Riemann Zeta Function

Imagine a sum that keeps getting bigger: 1 + 2 + 3 + 4 + ... but somehow, its "value" is said to be 

\[1+2+3+4+5… = -\frac{1}{12}\]
This equation isn’t a joke. It isn’t a typo. And it definitely isn’t like one of those internet tricks that try to prove that 2 = 3.

But how?

Doesn’t calculus dictate that the sum should diverge?

How can an infinite sum of positive integers result in a negative fraction?

This equation is one of the paradoxical results of the famed Riemann Zeta function: \[\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}\]

First Encounters

My first encounter of the Riemann Zeta function was in a problem introduced to me in Math circle India:\(\newline\)
    
        What is the probability that two random numbers x & y are coprime i.e. gcd(x,y) = 1 for \(  x,y \in \mathbb N\)

At first glance, it seems like an impossible question to compute. We’re picking 2 numbers at random — how do you even define a probability over an infinite set? There’s no upper limit, no finite set to compute over, yet there is a way to make sense of this idea. Not just a sense: an exact & surprising solution.

"To get there, let’s start by unpacking what it actually means for $x$ and $y$ to be co-prime." (two numbers are co-prime if they share no prime factors). Although we're dealing with an infinite set, we can think in terms of density. The probability of a number x being a multiple of p is \(\frac{1}{p}\) as every \(p^{th}\) number is a multiple of p. In continuation, the probability that 2 numbers x & y being multiples of p is \[\frac{1}{p}*\frac{1}{p} = \frac{1}{p^2}\] Therefore, the probability that both numbers are not multiples of p is \[1-\frac{1}{p^2}\]

To ensure that no prime divides both x and y, we need to exclude all such shared divisibility across every prime. So we multiply over all primes:

Therefore, \[P =\prod_{p \;prime} \left(1 - \frac{1}{p^2}\right)\] How does this relate to the zeta function?

Well, the zeta function is defined as \[\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}\] at s = 2, this equates to \[1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+…\]
At first glance, this looks nothing like a product over primes. However, the key insight comes from something called the Fundamental Theorem of Arithmetic. The theorem states that any number can be written as a product of prime powers. That is to say:  \(n = p_1^{n_1} \cdot p_2^{n_2} \cdot p_3^{n_3} ... \forall n \in \mathbb Z, p \in prime\).

Hence, \[\frac{1}{n^2} = \frac{1}{p_1^{2n_1} \cdot p_2^{2n_2} \cdot p_3^{2n_3} ...}\]
Therefore the sum \[1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+…\] can also be written as \[(1+\frac{1}{2^2}+\frac{1}{2^4}+\frac{1}{2^6}+...)(1+\frac{1}{3^2}+\frac{1}{3^4}+\frac{1}{3^6}+...)(1+\frac{1}{5^2}+\frac{1}{5^4}+\frac{1}{5^6}+...)...\] And here’s the surprising bit: even though it looks like we’re only summing specific prime powers, this product actually captures every single $\(\frac{1}{n^2}$\). For example, for \(\frac1{2^2}\) we multiply \(\frac1{2^2}\) from the first multiplicand with 1 from every other multiplicand. For \(\frac{1}{6^2}\) we multiply \(\frac 1{2^2}\) from the first multiplicand by \(\frac1{3^2}\) from the second multiplicand and 1 from every other. Similarly, we can form all \(\frac{1}{n^2}\), thus equating the two expressions. Further we take: \[(1+\frac{1}{2^2}+\frac{1}{2^4}+\frac{1}{2^6}+...)(1+\frac{1}{3^2}+\frac{1}{3^4}+\frac{1}{3^6}+...)(1+\frac{1}{5^2}+\frac{1}{5^4}+\frac{1}{5^6}+...)...\]\[=\prod_{p\;prime}(1+\frac{1}{p^2}+\frac{1}{p^4}+\frac{1}{p^6}+...)\]Notice that each one of these multiplicands is a geometric series with the common ratio of \(\frac1{p^2}\)\[\newline\]
Since \(\frac1{p^2}<1\):
\[\prod_{p\;prime}(1+\frac{1}{p^2}+\frac{1}{p^4}+\frac{1}{p^6}+...) = \prod_{p\;prime}\frac{1}{1-\frac{1}{p^2}}\]
Therefore\[\frac{1}{\zeta(2)} = \prod_{p\;prime}1-\frac{1}{p^2}\]
Therefore the probability of any two numbers being co-prime is\[P =\frac1{\zeta(2)} = \frac{6}{\pi^2}\] (The value of \(\zeta(2)\) comes from Euler's famous solution of the Basel problem). To me, this solution to a seemingly unsolvable problem is interesting not only because it contains the Riemann Zeta function, it also has a surprising to \(\pi\) and as a result, circles suggesting at a mystery conversation between the realms of geometry and number theory. 3Blue1Brown has an amazing video on this exact correlation linked here: https://youtu.be/d-o3eB9sfls?si=1LsDzTDFRQUyiBjv

Back to \(-\frac1{12}\)

This connection between the zeta function and prime numbers is only the beginning of a much deeper story. The Riemann zeta function can be extended to values of ss where the original series does not converge at all - like at s = -1, where the infinite sum 1+2+3+4+... obviously diverges. Yet, through a process called analytic continuation, the zeta function assigns this divergent sum a finite value: \(-\frac{1}{12}\)

A fun yet wrong way (similar to the various tricks on the internet that try to prove that 1=2) to get the desired result of \(-\frac{1}{12}\) is via manipulation of something known as the Grandi series. While this approach is wrong mathematically, it is still a fun exercise with infinite sets:

First, we take the set
\[1-1+1-1+1-1+...\]
Taking the sum \(S_1\) of the series we get three results!
\[S_1 = (1-1)+(1-1)+(1-1)+... = 0\]\[S_1 = 1-(1-1)-(1-1)... = 1\]
\[S_1 = 1-1+1-1+1-1+1-1...\]
\[2S_1 = 1-1+(1)+1-(1)-1+(1)+1-(1)-1+... = 1\]\[\Rightarrow S_1 = \frac{1}2\]The bracketed 1s are of the second \(S_1\)

In this, the first two equations are known as partial sums of the oscillating function.
Notice that the third sum is the average of the two partial sums also known as a Cesàro sum.

Next, we look at the series:
\[1-2+3-4+5-6+...\]
We calculate \(S_2\)
\[S_2 = 1-2+3-4+5-6+...\]\[2S_2 = 1-2+1+3-2-4+3+5-4-6+5+...\]\[\Rightarrow2S_2 = 1-1+1-1+1-1+... = S_1 = 1/2\]\[\Rightarrow S_2 = 1/4\]
Finally we take the series:\[S_3 = 1+2+3+4+5+6+...\]\[S_3+S_2 = 1+1+2-2+3+3+4-4+5+5+6-6+...\]
\[\Rightarrow S_3+S_2 = 2+6+10+14+18+...=2(1+3+5+7+9+...)\]
\[\Rightarrow S_3+S_2 = 2(S_3-2S_3)\]
\[\Rightarrow S_3 = -S_2/3 = -\frac{1}{4*3} = -\frac{1}{12}\]

Thus we get our miraculous result! However as I mentioned earlier, this solution is not correct. The reason for this is that we are treating divergent functions as convergent in the sense of adding and subtracting them. Moreover, as those who have studied calculus would agree, addition and subtraction of said infinities lie in the indeterminate form of limits as \(\infty-\infty\) can be anything: 0, a constant or even \(\infty\). While the Grandi-style manipulations are mathematically shaky, it is not true that \(-\frac{1}{12}\)is wrong too. It is actually a value that emerges not from set manipulations rather from a rigorous mathematical process called analytic continuation of the Riemann Zeta function.

More on the Riemann Zeta function:

So, what does \(-\frac{1}{12}\)actually mean then? While the Grandi-style manipulations are entertaining, they aren’t mathematically rigorous. The series 1+2+3+4+… diverges — it grows without bound — and no traditional method of summing it gives a finite result. However, this value of \(-\frac{1}{12}\) does appear in a rigorous way via complex analysis.

The Riemann Zeta function is defined to be \[\sum_{n=1}^{\infty}\frac{1}{n^s}\] The Riemann Zeta function is defined to be \[\sum_{n=1}^{\infty}\frac{1}{n^s}\] Which only converges when the real part of s, say s = a+bi, is greater than 1. For values of \(a \leq 1\), the series diverges.  So how do we get to values like \(\zeta(-1)\)? Analytic continuation.

In short, analytic continuation is the process of extending the graph for the complex function in such a way that it is continuous and differentiable for all values. But in order to complete graphs, we have to have the graph in the first place.

How do we make graphs for complex functions in a meaningful way? Complex functions take complex inputs and give complex outputs — which means both the input and the output each have two dimensions (real and imaginary parts). That’s a total of 4 dimensions! To visualize the complex function \(\zeta(s)\), we use a technique called grid transformation. This involves starting with a regular lattice (grid) on the complex plane — a set of horizontal and vertical lines marking points with fixed real and imaginary parts. We then apply the zeta function to each point on this grid, effectively mapping every input s to its corresponding output \(\zeta(s)\). As a result, the entire grid gets warped and transformed, revealing how the function stretches, twists, or compresses regions of the complex plane. The final image, like the one shown below, provides a powerful visual insight into the behavior of ζ(s)ζ(s) across the complex plane. 

 

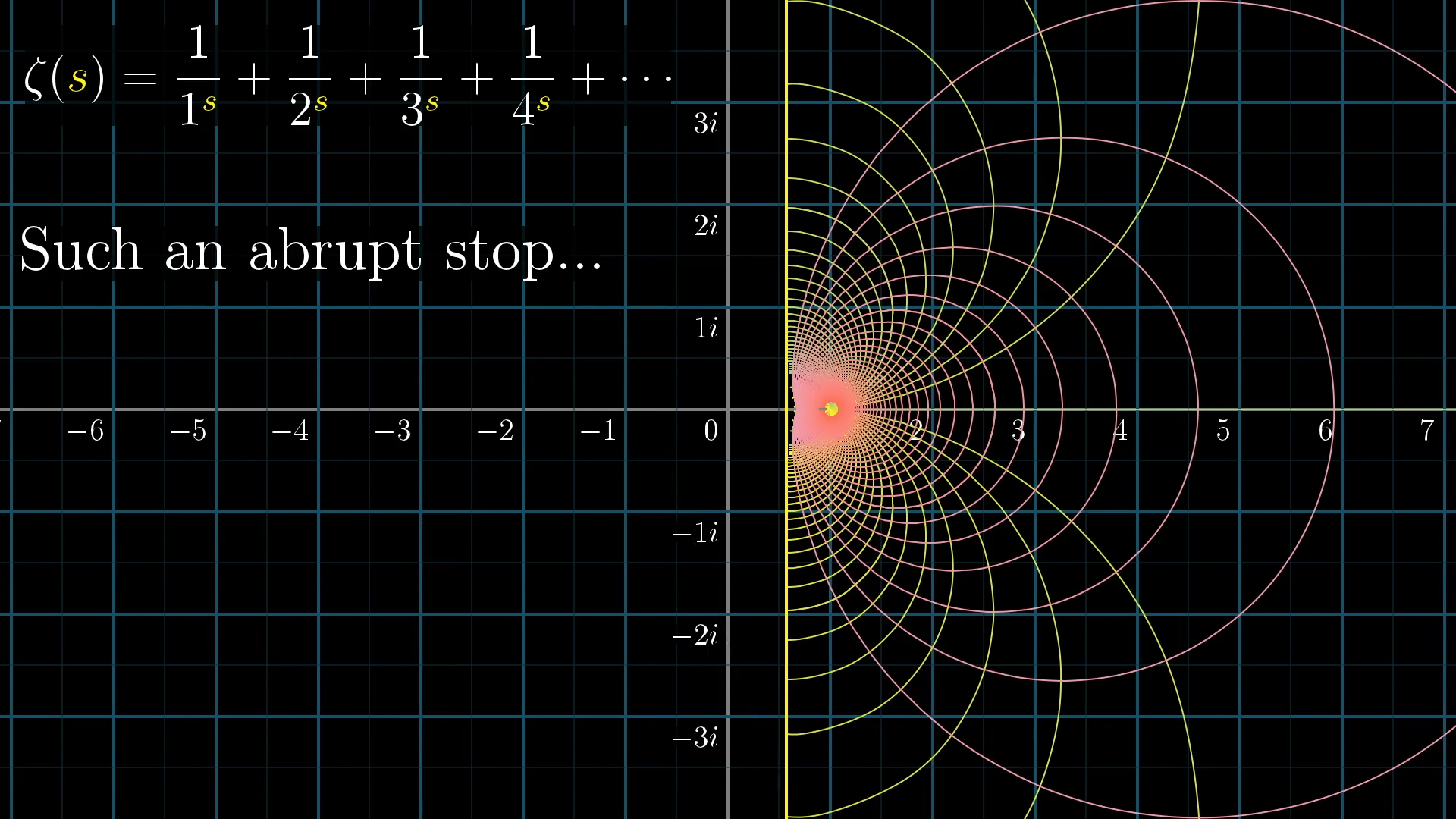
This graph however stops abruptly at the vertical line Re(s) = 1. This is where the concepts of analytical continuation comes in. Essentially, we extend the graph of \(\zeta(s)\) in such a way that it is both differentiable and continuous. However, this seems to lead to an infinite number of possibilities! To ensure that it is continuous, we just have to continue the graph without lifting our pencils and to ensure that it is differentiable, we just have to make sure that we draw no sharp corners right? Not quite. While that intuition works for real functions, we’re in the realm of complex analysis now — and the rules are a bit different. In the complex world, differentiability means much more than just being smooth. It implies something called holomorphicity, which requires the function to preserve angles and local shapes — a far stricter condition. So when we analytically continue \(\zeta(s)\), we’re not just sketching a visually smooth curve; we’re extending it in a way that maintains the angle-preserving structure across the complex plane. These constraints finally allow us to settle on a single shape for the graph of \(\zeta(s)\) as seen below.

 
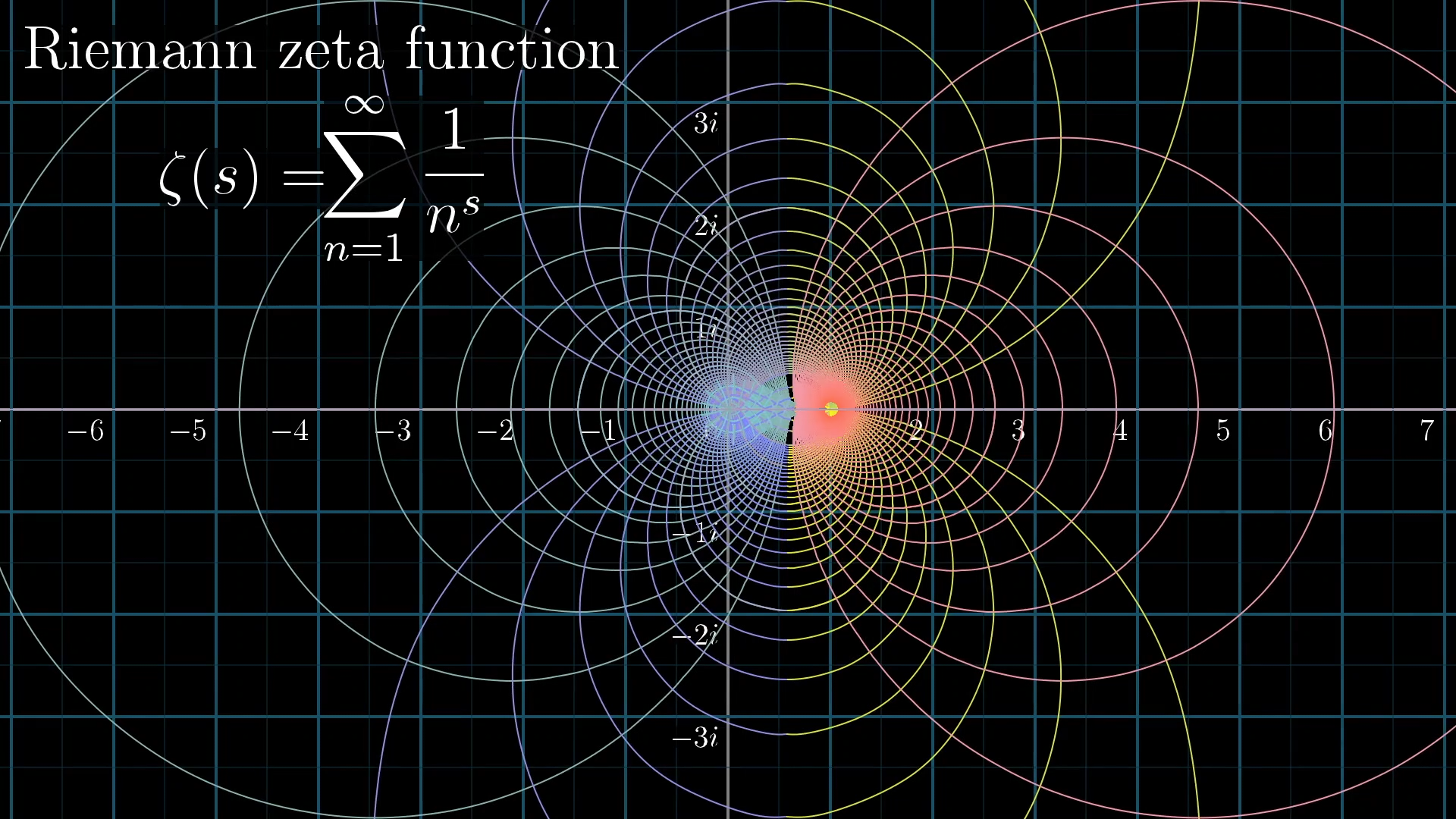
Moreover, this graph finally allows us to make sense of non trivial equations such as \[1+2+3+4+... = -\frac{1}{12}\] by plugging in values such as \(\zeta (-1)\) in our now complete graph.

Hence, we finish our journey to prove the nonsensical: An infinite sum of positive numbers can be a negative fraction. This is just a first glance into a strange and beautiful world of complex analysis, but it already feels like a playground of ideas. I would like to end by apologizing in advance on the rushed explanations at the end, they are the result of my relative inexperience to the field. In a way, I have been learning with you readers while writing this post

 

 

Credits:

Graphs by 3Blue1Brown